Grupo 16 Matematica LdeA
jueves, 24 de junio de 2021
Funciones Logaritmicas
martes, 22 de junio de 2021
Logaritmos
Logaritmos:
miércoles, 5 de mayo de 2021
Tipos de Limites
Tipos de Límites
Ahora daremos paso a los tipos de limites los cuales son:
- Límite de una función en un punto: El límite de la función f(x) es cuando X tiende a `a´ es el valor al que se aproxima la función, cuando la x se aproxima a `a´. A la izquierda, notación (Símbolo) utilizada referirnos al limite de una función en un punto cuando la `x´ se aproxima a `a´.
A continuación mostraremos algunos ejemplos sobre límites de una función en un punto
- Límite Finito e Infinito:
-Límite Finito:
Se dice que la función f(x), tiene Límite b, cuando x tiende a `a´, si dado ε positivo arbitrario y tan pequeño como se quiera.
Se dice que existe límite infinito cuando la función f(x) llega a valores que crecen continuamente, es decir que se puede hacer la función tan grande como queramos. Se dice que f(x) es diverge a infinito.
- Límite Laterales (izquierda y derecha):
La categoría de límites laterales se divide en dos tipos los cuales son izquierda y derecha, estos los representaremos como Izquierda L1 y representaremos como L2 a la derecha.
-Límite lateral por la Izquierda (L1):
Se denomina Límite por la Izquierda al que llamaremos L1 de una función definida f(x) en el intervalo abierto (a, c) y en un punto a, a la imagen, o el valor que toma esa función, cuando el valor de la variable x se acerca mucho a a, siendo x < a.
Se representa como:
Gráfica del Limite por la
izquierda.
-Gráfica del Límite por la derecha:
En la imagen de arriba se ve el concepto y notación del límite por la derecha. A medida que tomamos valores próximos a a, pero mayores que este (fondo verde oscuro), los correspondientes valores de f(x) se aproximan a L2. Decimos que L2 es el valor del límite de la función cuando x se aproxima a a por la derecha.
Veamos el ejercicio visto anteriormente, pero ahora cuando x tiende a 2 por la derecha, y encontremos el valor L2 (Límite lateral derecho).
Vemos que como los valores de x se aproximan a 2 por la derecha, la función en este caso se aproxima también por la derecha al límite lateral L2 (el valor 5).
Analicemos su tabla de valores:
Teorema de los límites laterales.
· Para que exista el límite de una función f(x) cuando x tiende a un punto dado, tienen que existir los dos límites laterales y ser iguales:
Es decir, para que exista el límite de una función cuando x tiende a un punto, L1 y L2 tienen que ser iguales.
· Cuando los límites por la izquierda y por la derecha de una función en un punto son distintos, no existe el límite de la función en dicho punto.
Tomemos como ejemplo los resultados de los ejercicios anteriores:
Como L1 y L2 son iguales, el limite de la función cuando x tiende a 2, existe.
martes, 4 de mayo de 2021
¿Que es el Limite de una Función?
¿Qué es el Limite de una Función?
El limite de una función se utiliza en el calculo diferencial matemático y refiere a la cercanía entre un valor y un punto. Por ejemplo:
Si una función `F´ tiene un limite `X´ en un punto `T´, quiere decir que el valor de F puede ser todo lo cercano a X, con puntos suficientemente cercanos a `T´.
viernes, 30 de abril de 2021
Tipos De Funciones
Tipos De Funciones
Ahora daremos paso a cada tipo de función, los cuales estaremos utilizando (Inyectiva, Sobreyectiva, Biyectiva, Lineal, Inversa) :
1) Función Inyectiva: Es una Función Inyectiva o también llamada ``Funciones Uno a uno´´ si a cada uno de los elementos del conjunto A le corresponde un elemento del conjunto B.
Ejemplo:
¿Que son las funciones?
Antes que nada debemos saber que es una función. Una función es una relación entre dos conjuntos los cuales son representados como A y B, de tal manera que a cada valor del primer conjunto (conocido como dominio) le corresponde un único valor de la segundo conjunto (llamado imagen).

Funciones Logaritmicas
Funciones Logarítmicas Una función logarítmica está conformada por un logaritmo de base a, y se demuestra de la siguiente forma: siendo a ...
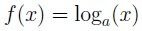
-
Tipos De Funciones Ahora daremos paso a cada tipo de función, los cuales estaremos utilizando (Inyectiva, Sobreyectiva, Biyectiva, Lineal, I...
-
Antes que nada debemos saber que es una función. Una función es una relación entre dos conjuntos los cuales son representados como A y B, ...
-
¿Qué es el Limite de una Función? El limite de una función se utiliza en el calculo diferencial matemático y refiere a la cercanía entre ...





































