Tipos De Funciones
Ahora daremos paso a cada tipo de función, los cuales estaremos utilizando (Inyectiva, Sobreyectiva, Biyectiva, Lineal, Inversa) :
1) Función Inyectiva: Es una Función Inyectiva o también llamada ``Funciones Uno a uno´´ si a cada uno de los elementos del conjunto A le corresponde un elemento del conjunto B.
Ejemplo:
Veamos que se cumple la condición de inyectividad:
En efecto, si xa y xb tienen la misma imagen, necesariamente deben ser el mismo elemento. Por lo tanto, f es inyectiva.
2)Función Sobreyectiva: Es una Función Sobreyectiva o también llamada ``Suprayectiva´´cuando todos los elementos del conjunto B tienen al menos un elemento del conjunto A.
3) Función Biyectiva: Es una función biyectiva cuando todos los elementos del conjunto A tienen una imagen distinta en el conjunto B, y a cada elemento del conjunto B le corresponde un elemento del conjunto A.
4) Función Lineal: Es una Función Polinómica de primer grado, es decir, una Función de una Variable (X), que puede ser escrita como la suma de términos de la forma `ax^n´.








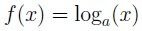


Me parece bien la explicación de cómo encontrar la función inversa de una dada. Creo que se debería decir que no todas las funciones tienen inversa, pero podemos "restringir la función" para que encontrar su inversa.
ResponderEliminarErika Castillo Espinoza
profesora de matemática