Funciones Logarítmicas
Una función logarítmica está conformada por un logaritmo de base a, y se demuestra de la siguiente forma:
siendo a un real positivo, a > 0, y diferente de 1, a ≠ 1.
Cuando 0 < a < 1, entonces la función logarítmica es una función decreciente y cuando a > 1, entonces es una función creciente.
Dominio: Son todos los números reales que provocan que el argumento de la función sea mayor que 0.
A continuación les presentaremos algunos ejemplos de dominios de funciones logarítmicas:
En este último caso, los reales negativos, junto con {0}+(0,2) son los que hacen el argumento mayor que cero.
Lo mismo ocurre cuando la base es menor que uno, que es cuando la función es decreciente.
El recorrido: ´´IR`` son todos los números reales.
Derivada de la función logarítmica elemental:.
Si a es mayor que 1 (a > 1), la función es estrictamente creciente. En cambio, si a es menor que 1 (a < 1), la función es estrictamente decreciente.
En la forma básica de la función, la imagen de 1 siempre es 0 sin importar cual sea la base a y la imagen de a es 1.
Así pues, las funciones logarítmicas, en su expresión simple, siempre pasan por los puntos (1 , 0) y (a , 1).










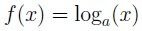


Muy bien compañeros me convence su trabajo
ResponderEliminar